理学部数学コース　勝呂 剛志

　統計⼒学や情報理論において, 状態の不確定性さや曖昧さを⽰す概念の⼀つとしてエントロピーが考えられています. 数学的には, いくつかの性質をみたす汎函数として⼀意的に定まることが知られています. ここでは, その連続版である次のエントロピー汎函数を考えます:

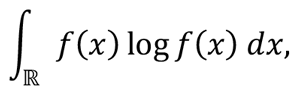
ここで, 函数 f(x) は任意の x ∈ ℝ に対して, f(x) ≥ 0 であり, ℝ 上可積分かつその積分値は1であると仮定します(これらの性質をみたす函数を確率密度函数と呼びます). このエントロピー汎函数は偏微分⽅程式・函数不等式と密接な関係を持っており, 本稿では, その関係性について簡単にまとめることにします.

　近年では, ⾃然科学に限らず, ⽇常⽣活に溢れるデータを確率分布として扱うことが多々あります. そういった``情報"を扱う際に, その乱雑さ・不確定さを測るエントロピー汎函数の振る舞いが焦点となりますが, そもそも, エントロピー汎函数が常に有界になるとは限りません. さらに, エントロピー汎函数は被積分函数に対数函数(の合成函数)を含むため符号が定まらず, エントロピー汎函数が上と下から有界になるための, 函数に課すべき条件を調べる必要があります. こういった研究は古くからなされており, エントロピー汎函数の有界性は函数不等式の形で, 下からの評価は C. E. Shannon によって, 上からの評価は A. J. Stam によって⽰されています. 特に後者は偏微分⽅程式の研究において⽤いられる Sobolev の不等式に対応して, 対数型 Sobolev の不等式と呼ばれています. 上と下からの両評価に通じる共通点として, 不等式の等号を達成する函数が確率論や統計学において現れる Gauss 函数(正規分布)となることが挙げられます. この函数は偏微分⽅程式の研究においても重要な函数であり, 特に, 偏微分⽅程式の⼀つである熱⽅程式の解であることが知られています(詳しくは, Pure Science 第12号の三沢正史先⽣の「偏微分⽅程式の数学」をご参照ください). さらに, 熱⽅程式の解に対するある評価が対数型 Sobolev の不等式と同値であることが知られています. こういった関連性は, エントロピー汎函数のある勾配流が熱⽅程式であるという観点から, 微分幾何学や機械学習の分野において⽤いられている最適輸送理論によって考察されています.

　数学において, 代数学, 幾何学, 解析学, 確率論等の様々な分野に跨った研究もあり, そういった⼀つの分野に限らず多岐の分野に興味を持つ学⽣が増えることを期待します.